
Here are the official and definitive results of the Ontology Alignment Evaluation 2005. A preliminary set of results has been unveiled in Banff, Canada, at the Kcap Ontology integration workshop.
A synthetic paper provides an organized view of these results. Here further data and update in the results are available. This page is the official result of the evaluation.
The papers provided by the participants have been collected in the Kcap Ontology integration workshop proceedings (PDF) which are also published as CEUR Workshop Proceedings volume 156.
Results have been computed from the files provided by the participants. However in order to be correctly processable, they went through some procedures that can be found here (in spite of its name, this procedure has been applied step by step by hand).
Because some alignments were not 1:1 alignments (and this had a large negative impact on the results), precision recall has not been computed by the 1.4 version of the Alignment API, but with 2.0 version. For those who submitted 1:1 alignments, the results given by both versions are the same.
A revised set of results have been provided for ctxMatch and included in these results. This is the only difference with the results presented in Banff.
We have suppressed test 102 from the alignments because we were unable to evaluate it. Many of you did not provided alignments for 102.
| algo | refalign | edna | falcon | foam | ctxMatch2-1 | dublin20 | cms | omap | ola | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| test | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. |
| 1xx | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 0.98 | 0.65 | 0.87 | 0.34 | 1.00 | 0.99 | 0.74 | 0.20 | 0.96 | 1.00 | 1.00 | 1.00 |
| 2xx | 1.00 | 1.00 | 0.41 | 0.56 | 0.90 | 0.89 | 0.89 | 0.69 | 0.72 | 0.19 | 0.94 | 0.71 | 0.81 | 0.18 | 0.31 | 0.68 | 0.80 | 0.73 |
| 3xx | 1.00 | 1.00 | 0.47 | 0.82 | 0.93 | 0.83 | 0.92 | 0.69 | 0.37 | 0.06 | 0.67 | 0.60 | 0.93 | 0.18 | 0.93 | 0.65 | 0.50 | 0.48 |
| H-mean | 1.00 | 1.00 | 0.45 | 0.61 | 0.91 | 0.89 | 0.90 | 0.69 | 0.72 | 0.20 | 0.92 | 0.72 | 0.81 | 0.18 | 0.35 | 0.70 | 0.80 | 0.74 |
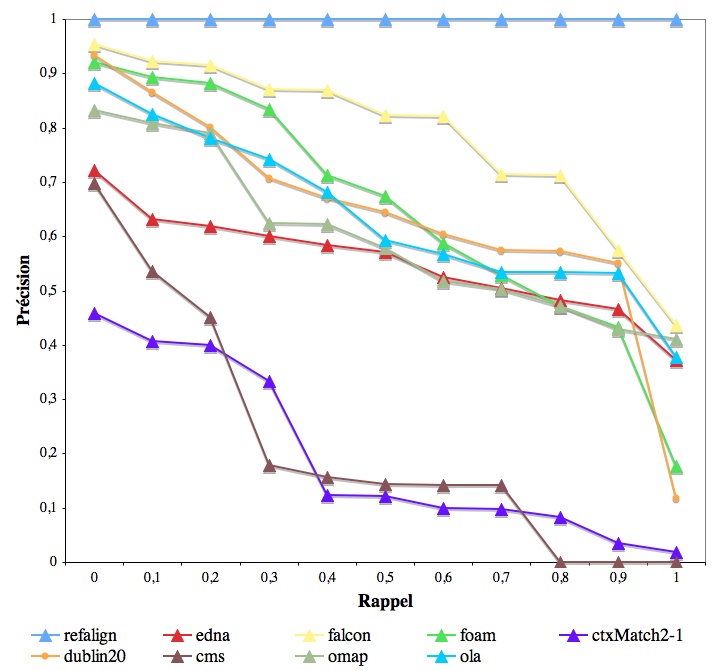
We display the results of participants as well as those given by some very simple edit distance algorithm on labels (edna corresponding to the class fr.inrialpes.exmo.align.impl.method.EditDistanceNameAlignment in the alignment API). The computed values here are real precision and recall and not a simple average of precision and recall. This is more accurate than what has been computed last year.
As can be seen, the 1xx tests are relatively easy for most of the participants. The 2xx tests are more difficult in general while 3xx tests are not significantly more difficult than 2xx for most participants. The real interesting results is that there are significant differences across algorithms within the 2xx test series.
Most of the best algorithms were combining different ways of finding the correspondence. Each of them is able to perform quite well on some tests with some methods. So the key issue seems to have been the combination of different methods (as described by the papers).
One algorithm, Falcon, seems largely dominant. But a group of other algorithms (Dublin, OLA, FOAM) are competing against each other, while the CMS and CtxMatch currently perform at a lower rate. Concerning these algorithm, CMS seems to priviledge precision and performs correctly in this (OLA seems to have privileged recall with regard to last year). CtxMatch has the difficulty of delivering many subsumption assertions. These assertions are taken by our evaluation procedure positively (even if equivalence assertions were required), but since there are many more assertions than in the reference alignments, this brings the result down.
Because of the precision/recall trade-off, as noted last year, it is difficult to compare the middle group of systems. In order to assess this, we attempted to draw precision recall graphs. We provide below the averaged precision and recall graphs of this year. They involve only the results of all participants. However, the results corresponding to participants who provided confidence measures equal to 1 or 0 can be considered as approximation (this is the case for ctxMatch, falcon and omap). Moreover, for reason of time these graphs have been computed by averaging the graphs of each tests (instead to pure precision and recall).

These graphs are not totally faithful to the algorithms because participants have cut their results (in order to get high overall precision and recall). They are also computed, for technical reasons, on average precision instead of true precision (this explain their generally higher precision).
However, they provide a rough idea about the way participants are fighting against each others in the precision recall space. It would be very useful that next year we ask for results with continuous ranking for drawing these kind of graphs.
Last year's figures have been recomputed with the current evaluator (especially for the average measures). The results can be found here:
| algo | karlsruhe2 | umontreal | fujitsu | stanford | ||||
|---|---|---|---|---|---|---|---|---|
| test | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. |
| 1xx | NaN | 0.00 | 0.57 | 0.93 | 0.99 | 1.00 | 0.99 | 1.00 |
| 2xx | 0.60 | 0.46 | 0.54 | 0.87 | 0.93 | 0.84 | 0.98 | 0.72 |
| 3xx | 0.90 | 0.59 | 0.36 | 0.57 | 0.60 | 0.72 | 0.93 | 0.74 |
| H-mean | 0.65 | 0.40 | 0.52 | 0.83 | 0.88 | 0.85 | 0.98 | 0.77 |
Corresponding results for this year are:
| algo | refalign | edna | falcon | foam | ctxMatch2-1 | dublin20 | cms | omap | ola | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| test | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. |
| 1xx | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 0.98 | 0.65 | 0.87 | 0.34 | 1.00 | 0.99 | 0.74 | 0.20 | 0.96 | 1.00 | 1.00 | 1.00 |
| 2xx | 1.00 | 1.00 | 0.66 | 0.72 | 0.98 | 0.97 | 0.87 | 0.73 | 0.79 | 0.23 | 0.98 | 0.92 | 0.91 | 0.20 | 0.89 | 0.79 | 0.89 | 0.86 |
| 3xx | 1.00 | 1.00 | 0.47 | 0.82 | 0.93 | 0.83 | 0.92 | 0.69 | 0.37 | 0.06 | 0.67 | 0.60 | 0.93 | 0.18 | 0.93 | 0.65 | 0.50 | 0.48 |
| H-mean | 1.00 | 1.00 | 0.72 | 0.78 | 0.98 | 0.98 | 0.89 | 0.72 | 0.81 | 0.25 | 0.98 | 0.93 | 0.87 | 0.20 | 0.90 | 0.84 | 0.91 | 0.89 |
These results can be compared with last year's results given above (with aggregated measures computed at new with the methods of this year). For the sake of comparison, the results of this year on the same test set as last year are given in above. As can be expected, the two participants of both challenges (Karlsruhe2 corresponding to foam and Montréal/INRIA corresponding to ola) have largely improved their results. The results of the best participants this year are over or similar to those of last year. This is remarkable, because participants did not tune their algorithms to the challenge of last year but to that of this year (more difficult since it contains more test of a more difficult nature and because of the addition of cycles in them).
So, it seem that the field is globally progressing.
| algo | refalign | edna | falcon | foam | ctxMatch2-1 | dublin20 | cms | omap | ola | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| test | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. | Prec. | Rec. |
| 101 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | n/a | n/a | 0.87 | 0.34 | 1.00 | 0.99 | n/a | n/a | 0.96 | 1.00 | 1.00 | 1.00 |
| 103 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 0.98 | 0.98 | 0.87 | 0.34 | 1.00 | 0.99 | 0.67 | 0.25 | 0.96 | 1.00 | 1.00 | 1.00 |
| 104 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 0.98 | 0.98 | 0.87 | 0.34 | 1.00 | 0.99 | 0.80 | 0.34 | 0.96 | 1.00 | 1.00 | 1.00 |
| 201 | 1.00 | 1.00 | 0.03 | 0.03 | 0.98 | 0.98 | n/a | n/a | 0.00 | 0.00 | 0.96 | 0.96 | 1.00 | 0.07 | 0.80 | 0.38 | 0.71 | 0.62 |
| 202 | 1.00 | 1.00 | 0.03 | 0.03 | 0.87 | 0.87 | 0.79 | 0.52 | 0.00 | 0.00 | 0.75 | 0.28 | 0.25 | 0.01 | 0.82 | 0.24 | 0.66 | 0.56 |
| 203 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.87 | 0.34 | 1.00 | 0.99 | 1.00 | 0.24 | 0.96 | 1.00 | 1.00 | 1.00 |
| 204 | 1.00 | 1.00 | 0.90 | 0.94 | 1.00 | 1.00 | 1.00 | 0.97 | 0.87 | 0.28 | 0.98 | 0.98 | 1.00 | 0.24 | 0.93 | 0.89 | 0.94 | 0.94 |
| 205 | 1.00 | 1.00 | 0.34 | 0.35 | 0.88 | 0.87 | 0.89 | 0.73 | 0.36 | 0.04 | 0.98 | 0.97 | 1.00 | 0.09 | 0.58 | 0.66 | 0.43 | 0.42 |
| 206 | 1.00 | 1.00 | 0.51 | 0.54 | 1.00 | 0.99 | 1.00 | 0.82 | 0.30 | 0.03 | 0.96 | 0.95 | 1.00 | 0.09 | 0.74 | 0.49 | 0.94 | 0.93 |
| 207 | 1.00 | 1.00 | 0.51 | 0.54 | 1.00 | 0.99 | 0.96 | 0.78 | 0.30 | 0.03 | 0.96 | 0.95 | 1.00 | 0.09 | 0.74 | 0.49 | 0.95 | 0.94 |
| 208 | 1.00 | 1.00 | 0.90 | 0.94 | 1.00 | 1.00 | 0.96 | 0.89 | 0.87 | 0.28 | 0.99 | 0.96 | 1.00 | 0.19 | 0.96 | 0.90 | 0.94 | 0.94 |
| 209 | 1.00 | 1.00 | 0.35 | 0.36 | 0.86 | 0.86 | 0.78 | 0.58 | 0.36 | 0.04 | 0.68 | 0.56 | 1.00 | 0.04 | 0.41 | 0.60 | 0.43 | 0.42 |
| 210 | 1.00 | 1.00 | 0.51 | 0.54 | 0.97 | 0.96 | 0.87 | 0.64 | 0.40 | 0.04 | 0.96 | 0.82 | 0.82 | 0.09 | 0.88 | 0.39 | 0.95 | 0.94 |
| 221 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.87 | 0.34 | 1.00 | 0.99 | 1.00 | 0.27 | 0.96 | 1.00 | 1.00 | 1.00 |
| 222 | 1.00 | 1.00 | 0.91 | 0.99 | 1.00 | 1.00 | 0.98 | 0.98 | 0.73 | 0.26 | 1.00 | 0.99 | 1.00 | 0.23 | 0.96 | 1.00 | 1.00 | 1.00 |
| 223 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 0.99 | 0.98 | 0.83 | 0.31 | 0.99 | 0.98 | 0.96 | 0.26 | 0.96 | 1.00 | 1.00 | 1.00 |
| 224 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.87 | 0.34 | 1.00 | 0.99 | 1.00 | 0.27 | 0.96 | 1.00 | 1.00 | 1.00 |
| 225 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.84 | 0.32 | 1.00 | 0.99 | 0.74 | 0.26 | 0.96 | 1.00 | 1.00 | 1.00 |
| 228 | 1.00 | 1.00 | 0.38 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.92 | 1.00 | 1.00 | 1.00 | 0.74 | 0.76 | 0.92 | 1.00 | 1.00 | 1.00 |
| 230 | 1.00 | 1.00 | 0.71 | 1.00 | 0.94 | 1.00 | 0.94 | 1.00 | 0.83 | 0.35 | 0.95 | 0.99 | 1.00 | 0.26 | 0.89 | 1.00 | 0.95 | 0.97 |
| 231 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 0.98 | 0.98 | 0.87 | 0.34 | 1.00 | 0.99 | 1.00 | 0.27 | 0.96 | 1.00 | 1.00 | 1.00 |
| 232 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.84 | 0.32 | 1.00 | 0.99 | 1.00 | 0.27 | 0.96 | 1.00 | 1.00 | 1.00 |
| 233 | 1.00 | 1.00 | 0.38 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.55 | 0.52 | 1.00 | 1.00 | 0.81 | 0.76 | 0.92 | 1.00 | 1.00 | 1.00 |
| 236 | 1.00 | 1.00 | 0.38 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.86 | 0.94 | 1.00 | 1.00 | 0.74 | 0.76 | 0.92 | 1.00 | 1.00 | 1.00 |
| 237 | 1.00 | 1.00 | 0.91 | 0.99 | 1.00 | 1.00 | 1.00 | 0.99 | 0.79 | 0.29 | 1.00 | 0.99 | 1.00 | 0.23 | 0.95 | 1.00 | 0.97 | 0.98 |
| 238 | 1.00 | 1.00 | 0.96 | 1.00 | 0.99 | 0.99 | 1.00 | 0.99 | 0.76 | 0.29 | 0.99 | 0.98 | 0.96 | 0.26 | 0.96 | 1.00 | 0.99 | 0.99 |
| 239 | 1.00 | 1.00 | 0.28 | 1.00 | 0.97 | 1.00 | 0.97 | 1.00 | 0.74 | 0.79 | 0.97 | 1.00 | 0.71 | 0.76 | 0.85 | 1.00 | 0.97 | 1.00 |
| 240 | 1.00 | 1.00 | 0.33 | 1.00 | 0.97 | 1.00 | 0.94 | 0.97 | 0.78 | 0.85 | 0.94 | 0.97 | 0.71 | 0.73 | 0.87 | 1.00 | 0.97 | 1.00 |
| 241 | 1.00 | 1.00 | 0.38 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.58 | 0.58 | 1.00 | 1.00 | 0.81 | 0.76 | 0.92 | 1.00 | 1.00 | 1.00 |
| 246 | 1.00 | 1.00 | 0.28 | 1.00 | 0.97 | 1.00 | 0.97 | 1.00 | 0.75 | 0.83 | 0.97 | 1.00 | 0.71 | 0.76 | 0.85 | 1.00 | 0.97 | 1.00 |
| 247 | 1.00 | 1.00 | 0.33 | 1.00 | 0.94 | 0.97 | 0.94 | 0.97 | 0.77 | 0.82 | 0.94 | 0.97 | 0.71 | 0.73 | 0.87 | 1.00 | 0.97 | 1.00 |
| 248 | 1.00 | 1.00 | 0.06 | 0.06 | 0.84 | 0.82 | 0.89 | 0.51 | 0.00 | 0.00 | 0.71 | 0.25 | 0.25 | 0.01 | 0.82 | 0.24 | 0.59 | 0.46 |
| 249 | 1.00 | 1.00 | 0.04 | 0.04 | 0.86 | 0.86 | 0.80 | 0.51 | 0.00 | 0.00 | 0.74 | 0.29 | 0.25 | 0.01 | 0.81 | 0.23 | 0.59 | 0.46 |
| 250 | 1.00 | 1.00 | 0.01 | 0.03 | 0.77 | 0.70 | 1.00 | 0.55 | 0.00 | 0.00 | 1.00 | 0.09 | 0.00 | 0.00 | 0.05 | 0.45 | 0.30 | 0.24 |
| 251 | 1.00 | 1.00 | 0.01 | 0.01 | 0.69 | 0.69 | 0.90 | 0.41 | 0.00 | 0.00 | 0.79 | 0.32 | 0.25 | 0.01 | 0.82 | 0.25 | 0.42 | 0.30 |
| 252 | 1.00 | 1.00 | 0.01 | 0.01 | 0.67 | 0.67 | 0.67 | 0.35 | 0.00 | 0.00 | 0.57 | 0.22 | 0.25 | 0.01 | 0.82 | 0.24 | 0.59 | 0.52 |
| 253 | 1.00 | 1.00 | 0.05 | 0.05 | 0.86 | 0.85 | 0.80 | 0.40 | 0.00 | 0.00 | 0.76 | 0.27 | 0.25 | 0.01 | 0.81 | 0.23 | 0.56 | 0.41 |
| 254 | 1.00 | 1.00 | 0.02 | 0.06 | 1.00 | 0.27 | 0.78 | 0.21 | 0.00 | 0.00 | NaN | 0.00 | 0.00 | 0.00 | 0.03 | 1.00 | 0.04 | 0.03 |
| 257 | 1.00 | 1.00 | 0.01 | 0.03 | 0.70 | 0.64 | 1.00 | 0.64 | 0.00 | 0.00 | 1.00 | 0.09 | 0.00 | 0.00 | 0.05 | 0.45 | 0.25 | 0.21 |
| 258 | 1.00 | 1.00 | 0.01 | 0.01 | 0.70 | 0.70 | 0.88 | 0.39 | 0.00 | 0.00 | 0.79 | 0.32 | 0.25 | 0.01 | 0.82 | 0.25 | 0.49 | 0.35 |
| 259 | 1.00 | 1.00 | 0.01 | 0.01 | 0.68 | 0.68 | 0.61 | 0.34 | 0.00 | 0.00 | 0.59 | 0.21 | 0.25 | 0.01 | 0.82 | 0.24 | 0.58 | 0.47 |
| 260 | 1.00 | 1.00 | 0.00 | 0.00 | 0.52 | 0.48 | 0.75 | 0.31 | 0.00 | 0.00 | 0.75 | 0.10 | 0.00 | 0.00 | 0.05 | 0.86 | 0.26 | 0.17 |
| 261 | 1.00 | 1.00 | 0.00 | 0.00 | 0.50 | 0.48 | 0.63 | 0.30 | 0.00 | 0.00 | 0.33 | 0.06 | 0.00 | 0.00 | 0.01 | 0.15 | 0.14 | 0.09 |
| 262 | 1.00 | 1.00 | 0.01 | 0.03 | 0.89 | 0.24 | 0.78 | 0.21 | 0.00 | 0.00 | NaN | 0.00 | 0.00 | 0.00 | 0.03 | 1.00 | 0.20 | 0.06 |
| 265 | 1.00 | 1.00 | 0.00 | 0.00 | 0.48 | 0.45 | 0.75 | 0.31 | 0.00 | 0.00 | 0.75 | 0.10 | 0.00 | 0.00 | 0.05 | 0.86 | 0.22 | 0.14 |
| 266 | 1.00 | 1.00 | 0.00 | 0.00 | 0.50 | 0.48 | 0.67 | 0.36 | 0.00 | 0.00 | 0.33 | 0.06 | 0.00 | 0.00 | 0.01 | 0.15 | 0.14 | 0.09 |
| 301 | 1.00 | 1.00 | 0.48 | 0.79 | 0.96 | 0.80 | 0.83 | 0.31 | 0.00 | 0.00 | 0.74 | 0.64 | 1.00 | 0.13 | 0.94 | 0.25 | 0.42 | 0.38 |
| 302 | 1.00 | 1.00 | 0.31 | 0.65 | 0.97 | 0.67 | 0.97 | 0.65 | 0.00 | 0.00 | 0.62 | 0.48 | 1.00 | 0.17 | 1.00 | 0.58 | 0.37 | 0.33 |
| 303 | 1.00 | 1.00 | 0.40 | 0.82 | 0.80 | 0.82 | 0.89 | 0.80 | 0.32 | 0.14 | 0.51 | 0.53 | 1.00 | 0.18 | 0.93 | 0.80 | 0.41 | 0.49 |
| 304 | 1.00 | 1.00 | 0.71 | 0.95 | 0.97 | 0.96 | 0.95 | 0.96 | 0.58 | 0.09 | 0.75 | 0.70 | 0.85 | 0.22 | 0.91 | 0.91 | 0.74 | 0.66 |
| H-mean | 1.00 | 1.00 | 0.45 | 0.61 | 0.91 | 0.89 | 0.90 | 0.69 | 0.72 | 0.20 | 0.92 | 0.72 | 0.81 | 0.18 | 0.35 | 0.70 | 0.80 | 0.74 |
As general comments, we remark that it is still difficult for participants to provide results that correspond to the challenge (incorrect format, alignment with external entities). Because time is short and we try to avoid modifying provided results, this test is still a test of both algorithms and their ability to deliver a required format. However, some teams are really performant in this (and the same teams generally have their tools validated relatively easily).
The evaluation of algorithms like ctxMatch which provide many subsumption assertions is relatively inadequate. Even if the test can remain a test of inference equivalence. It would be useful to be able to count adequately, i.e., not negatively for precision, true assertions like owl:Thing subsuming another concept. We must develop new evaluation methods taken into account these assertions and the semantics of the OWL language.
As a side note: all participants but one have used the UTF-8 version of the tests, so next time, this one will have to be the standard one with iso-latin as an exception.
Here are all the error message obtained when evaluating the complete set of tests. They are given for the sake of completeness.
$ java -Xmx1200m -cp $JAVALIB/procalign.jar fr.inrialpes.exmo.align.util.GroupEval -c -l $FILES > ../results.html org.xml.sax.SAXParseException: Document root element is missing. java.io.FileNotFoundException: /Volumes/Phata/OAEI-2005/MERGED/101/cms.rdf (No such file or directory) org.xml.sax.SAXParseException: Expected "" to terminate element starting on line 9. Warning (cell voided), missing entity [OWLClassImpl] http://oaei.inrialpes.fr/2005/benchmarks/101/onto.rdf#Misc null Warning (cell voided), missing entity [OWLClassImpl] http://oaei.inrialpes.fr/2005/benchmarks/101/onto.rdf#Book null Warning (cell voided), missing entity [OWLClassImpl] http://oaei.inrialpes.fr/2005/benchmarks/101/onto.rdf#Conference null Warning (cell voided), missing entity [OWLClassImpl] http://oaei.inrialpes.fr/2005/benchmarks/101/onto.rdf#Book null Warning (cell voided), missing entity [OWLClassImpl] http://oaei.inrialpes.fr/2005/benchmarks/101/onto.rdf#Conference null Warning (cell voided), missing entity [OWLClassImpl] http://oaei.inrialpes.fr/2005/benchmarks/101/onto.rdf#Misc null Warning (cell voided), missing entity [OWLClassImpl] http://oaei.inrialpes.fr/2005/benchmarks/101/onto.rdf#Conference null Warning (cell voided), missing entity [OWLClassImpl] http://oaei.inrialpes.fr/2005/benchmarks/101/onto.rdf#Book null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity null null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null Warning (cell voided), missing entity [OWLClassImpl] http://www.w3.org/2002/07/owl#Thing null
Alignment files provided by the participants have been compared to the reference alignments that can be obtained in this mappings.zip file. As explained in the synthesis paper, only recall results are available.
The methodology used for the evaluation is detailled in Paulo Avesani, Fausto Giunchiglia, Mikalai Yatskevich, A Large Scale Taxonomy Mapping Evaluation, Proceedings of International Semantic Web Conference (ISWC), pp67-81, 2005.
The results for web directory matching task are presented on the following figure. As from the figure the web directories matching task is a very hard one. In fact the best systems found about 30% of mappings form the dataset (i.e., have Recall about 30%).
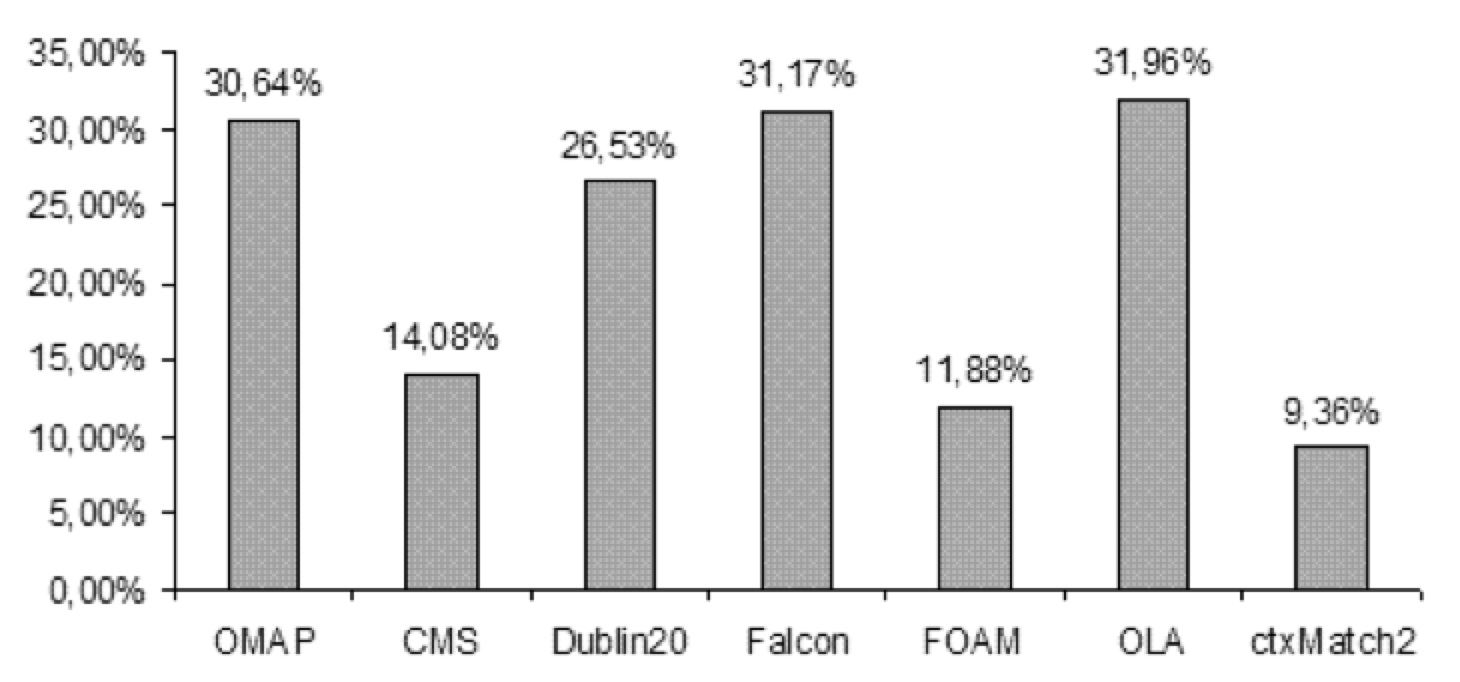
The results of the evaluation give us some evidence for complexity and discrimination capability properties. As from the following figure TaxME dataset is hard for state of the art matching techniques since there are no systems having recall more than 35% on the dataset. At the same time all the matching systems together found about 60% of mappings. This means that there is a big space for improvements for state of the art matching solutions.
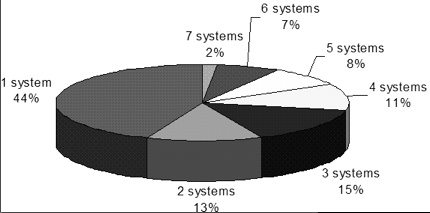
The figure contains partitioning of the mappings found by the matching systems. As from the figure 44% of the mappings found by any of the matching systems was found by only one system. This is a good argument to the dataset discrimination capability property.
The web directories matching task is an important step towards evaluation on the real world matching problems. At the same time there are a number of limitations which makes the task only an intermediate step. First of all the current version of the mapping dataset provides correct but not complete set of reference mappings. The new mapping dataset construction techniques can overcome this limitation. In the evaluation the mapping task was split to the the tiny subtasks. This strategy allowed to obtain results form all the matching systems participating in the evaluation. At the same time it hides computational complexity of "real world" matching (the web directories have up to $10^5$ nodes) and may affect the results of the tools relying on "look for similar siblings" heuristic.
The results obtained on the web directories matching task coincide well with previously reported results on the same dataset. According to \cite{taxme} generic matching systems (or the systems intended to match any graph-like structures) have Recall from 30% to 60% on the dataset. At the same time the real world matching tasks are very hard for state of the art matching systems and there is a huge space for improvements in the ontology matching techniques.
At the time of printing we are not able to provide results of evaluation on this test.
Validation of the results on the medical ontologies matching task is still an open problem. The results can be replicated in straightforward way. At the same time there are no sufficiently big set of the reference mappings what makes impossible calculation of the matching quality measures.
We are currently developing an approach for creating such a set.